データ構造と代数構造への招待

みなさま、お疲れ様です！エンジニア採用広報の高瀬 (@Guvalif) です。

この記事は、Chatwork Advent Calendar 2020 における、16 日目の記事です。

Chatwork にはたくさんの部活動があるのですが、その中に「数学部」という部活があります。

この記事は、数学部の活動として定期的に実施していた社内圏論勉強会からスピンオフして、「さまざまなデータ構造の背景にある、数学的な構造」を、わかりやすーく (≒ No ほむほむ*1に) 紹介してみるものです。

I. 参考文献のご紹介
II. データのまとまりとはなんだろう？
III. 適切なモデルを考える
IV. 2 つの列は同じもの？
V. 連結操作に代数構造を加える
VI. 代数構造を変えれば、データ構造も変わる
VII. まとめ

I. 参考文献のご紹介

まず本題に入る前に、この記事の元となった資料をご紹介します：

nineties.github.io

こちらは、@9_ties さんが 2013 年に実施していた圏論勉強会から、第 3 回『様々な圏』より "自由対象" の章を抜き出したものです。

これら一連の資料はとても出来が良く、数学的厳密性を犠牲にすることなく、関数型プログラミングが好きなエンジニアにとって身近な例がたくさん紹介されています。

一方で、ある程度専門的な数学知識を要求する部分もあり、じっくりと考えて行間を埋めることも、時に必要となっているように思います。

この記事は、該当の章 (およびその周辺) のサーベイ記事を目指したものになります 👨‍🏫

II. データのまとまりとはなんだろう？

エンジニアであれば、複数のデータをまとめるために "配列"*2 を使ったことがあるでしょう。しかし、これをきちんと数学的に定義しようとすると、意外と難しいことに気づきます。

「ん？集合を使えばデータのまとまりを表現できるのでは？？ 🤔」と考えたあなた，次の例を見てみましょう：

集合 $\mathbb{X}$ を、配列と考えてみる
集合 $\mathbb{X}$ には、3 つの数値データ 0, 1, 2 が順番に収められているとする
Q. ここで、新たに数値データ 0 を集合 $\mathbb{X}$ に追加すると、どうなるか？

f:id:cw-takase:20201215000935p:plain

われわれの勝手知ったる配列であれば、これは [ 0, 1, 2, 0 ] のようになって欲しいところです。しかし残念なことに、数学的な集合 $\mathbb{X}$ では [ 0, 1, 2 ] となってしまいます。

さらにいえば、[ 0, 1, 2 ] と [ 2, 1, 0 ] のような、収める順番が異なるもの同士も区別されません！

f:id:cw-takase:20201215000939p:plain

なぜそうなるのでしょうか？理由は次の通りです：

数学的な集合では、同一な要素は区別されず、1 つとして管理される
数学的な集合では、どの要素が含まれるかだけが重要であり、順番という概念は無い

III. 適切なモデルを考える

さて、数学的な集合をただ単に用いるだけでは、配列といったありふれたデータ構造でさえ、表現できないことが明らかになりました 💀

しかし諦める必要はありません。適切な取り扱いができる限り、数学ではルールを自由に考えてよいのです！ 🎉

というわけで、配列を数学的に扱うために、次のようなモデルを考えてみましょう：

任意のデータ $x$ に対して、単一データのまとまりを $|x|$ と表すことにする
$|x|$ のことを、"列" と呼ぶことにする
2 つの列 $|x|$ と $|y|$ に対して、連結操作 (演算子) $\oplus$ を考える
連結結果は $|x| \oplus |y|$ で表され、これもまた "列" であるとする

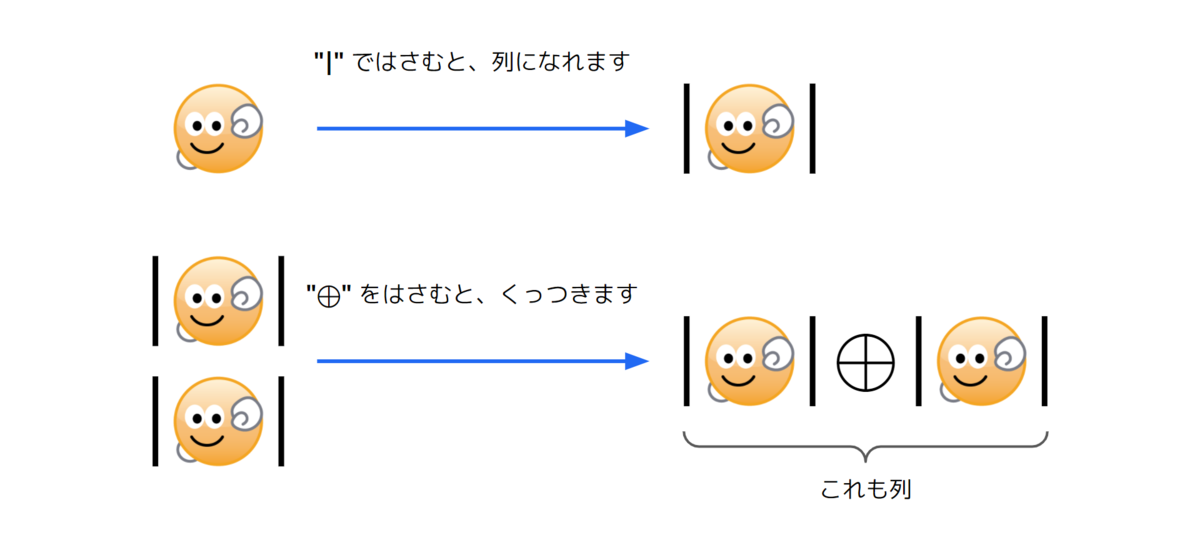
f:id:cw-takase:20201215000943p:plain

小難しい書き方をしましたが、ようするに数学的な表現で、なんらかデータを並べる方法を定義したと思えば良いです。

これも …　 $|0|$
あれも …　 $|0| \oplus |1|$
それも …　 $(|0| \oplus |1|) \oplus |0|$

どれもがデータの並びを表現していて、なおかつ集合という概念に頼っていないので、同一の要素を区別してくれないとか、順番が無視されるということがありません。素晴らしいですね 😊

IV. 2 つの列は同じもの？

さて、列と連結操作という考え方により、複数のデータをうまく並べることができるようになりました。

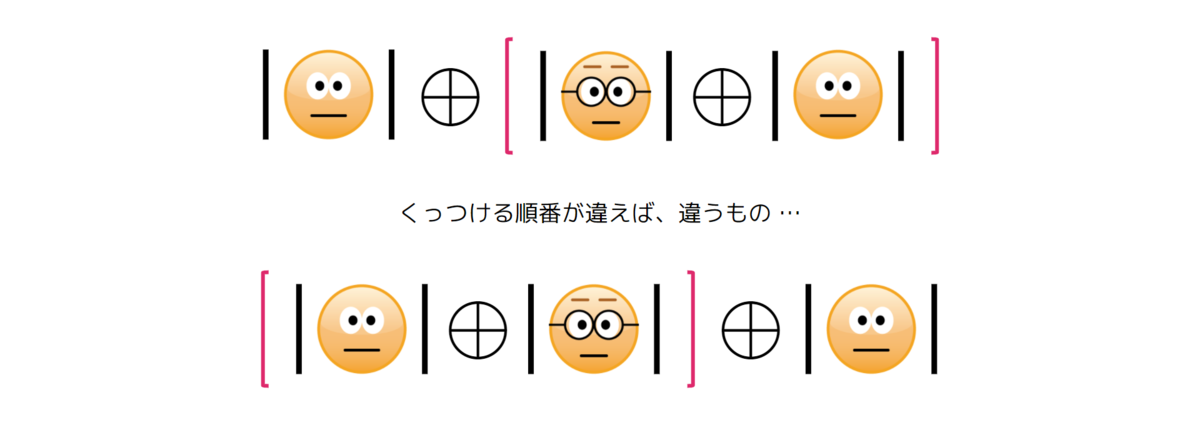
ではここで、3 つの数値データ 0, 1, 2 が順番に収められている列を考えてみましょう：

$(|0| \oplus |1|) \oplus |2|$
$|0| \oplus (|1| \oplus |2|)$

… 2 つできてしまいました 😅

「ん？こんなのカッコを外したら一緒なのでは？？ 🤔」と考えたあなた，そんなルールは与えていないのです。

任意のデータ $x$ に対して、単一データのまとまりを $|x|$ と表すことにする

$|x|$ のことを、"列" と呼ぶことにする

2 つの列 $|x|$ と $|y|$ に対して、連結操作 (演算子) $\oplus$ を考える

連結結果は $|x| \oplus |y|$ で表され、これもまた "列" であるとする

… どうでしょう？「カッコは自由に外していいよー」なんてルールはありませんね？*3

f:id:cw-takase:20201215172106p:plain